二分查找包括求查找中间值和左右边界值三种情况。
二分查找(左右指针)模板
左右指针即为最开始,左指针left在数组的最开始位置,右指针right在数组的末尾,然后循环时在判断左右指针什么时候开始相向移动,直至left == right左右指针相遇。
常见题目:二分查找,求两数之和、反转数组等。
重点为二分查找,二分查找的数组可能包含重复值,重复值的寻找条件可能包含第一寻找到相同元素返回、寻找指定元素的最左边界位置、寻找指定元素的最右边界位置等三种情况。三种边界的区别在于,寻找到指定元素后是否需要第一时间返回位置值,即nums[mid]==target时的操作不同,可见下列算法。
算法如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| int binary_search(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while(left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if(nums[mid] == target) {
return mid;
}
}
return -1;
}
int left_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
right = mid - 1;
}
}
if (left < 0 || left >= nums.length) {
return -1;
}
return nums[left] == target ? left : -1;
}
int right_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
left = mid + 1;
}
}
if (right < 0 || right >= nums.length) {
return -1;
}
return nums[right] == target ? right : -1;
}
|
2300.咒语和药水的成功对数(中等)
Problem: 2300. 咒语和药水的成功对数
给你两个正整数数组 spells 和 potions ,长度分别为 n 和 m ,其中 spells[i] 表示第 i 个咒语的能量强度,potions[j] 表示第 j 瓶药水的能量强度。
同时给你一个整数 success 。一个咒语和药水的能量强度 相乘 如果 大于等于 success ,那么它们视为一对 成功 的组合。
请你返回一个长度为 n 的整数数组 pairs,其中 pairs[i] 是能跟第 i 个咒语成功组合的 药水 数目。
示例 1:
输入:spells = [5,1,3], potions = [1,2,3,4,5], success = 7
输出:[4,0,3]
解释:
- 第 0 个咒语:5 * [1,2,3,4,5] = [5,10,15,20,25] 。总共 4 个成功组合。
- 第 1 个咒语:1 * [1,2,3,4,5] = [1,2,3,4,5] 。总共 0 个成功组合。
- 第 2 个咒语:3 * [1,2,3,4,5] = [3,6,9,12,15] 。总共 3 个成功组合。
所以返回 [4,0,3] 。
示例 2:
输入:spells = [3,1,2], potions = [8,5,8], success = 16
输出:[2,0,2]
解释:
- 第 0 个咒语:3 * [8,5,8] = [24,15,24] 。总共 2 个成功组合。
- 第 1 个咒语:1 * [8,5,8] = [8,5,8] 。总共 0 个成功组合。
- 第 2 个咒语:2 * [8,5,8] = [16,10,16] 。总共 2 个成功组合。
所以返回 [2,0,2] 。
提示:
n == spells.lengthm == potions.length1 <= n, m <= 1051 <= spells[i], potions[i] <= 1051 <= success <= 1010
思路
刚看的时候想到暴力A,但是第52个用例开始超时,所以改用二分法,找到排序后的药水最左边满足条件的下标,n - left 为第 i 个魔法成功的对数。
解题方法
对药水进行递增排序,然后二分查找满足 success 的药水下标。
复杂度
时间复杂度:(不算sort)
$O(mlogn)$
空间复杂度:
$O(n)$
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| class Solution {
public int[] successfulPairs(int[] spells, int[] potions, long success) {
int m = spells.length, n = potions.length;
Arrays.sort(potions);
int[] res = new int[m];
for (int i = 0; i < m; i++) {
int l = 0, r = n - 1;
while(l <= r) {
int mid = l + (r - l) / 2;
long check = (long)spells[i] * (long)potions[mid];
if (check < success) {
l = mid + 1;
} else {
r = mid - 1;
}
}
res[i] = n - l;
}
return res;
}
}
|
2258. 逃离火灾(困难)
图+BFS+二分查找
Problem: 2258. 逃离火灾
给你一个下标从 0 开始大小为 m x n 的二维整数数组 grid ,它表示一个网格图。每个格子为下面 3 个值之一:
0 表示草地。1 表示着火的格子。2 表示一座墙,你跟火都不能通过这个格子。
一开始你在最左上角的格子 (0, 0) ,你想要到达最右下角的安全屋格子 (m - 1, n - 1) 。每一分钟,你可以移动到 相邻 的草地格子。每次你移动 之后 ,着火的格子会扩散到所有不是墙的 相邻 格子。
请你返回你在初始位置可以停留的 最多 分钟数,且停留完这段时间后你还能安全到达安全屋。如果无法实现,请你返回 -1 。如果不管你在初始位置停留多久,你 总是 能到达安全屋,请你返回 109 。
注意,如果你到达安全屋后,火马上到了安全屋,这视为你能够安全到达安全屋。
如果两个格子有共同边,那么它们为 相邻 格子。
示例 1:
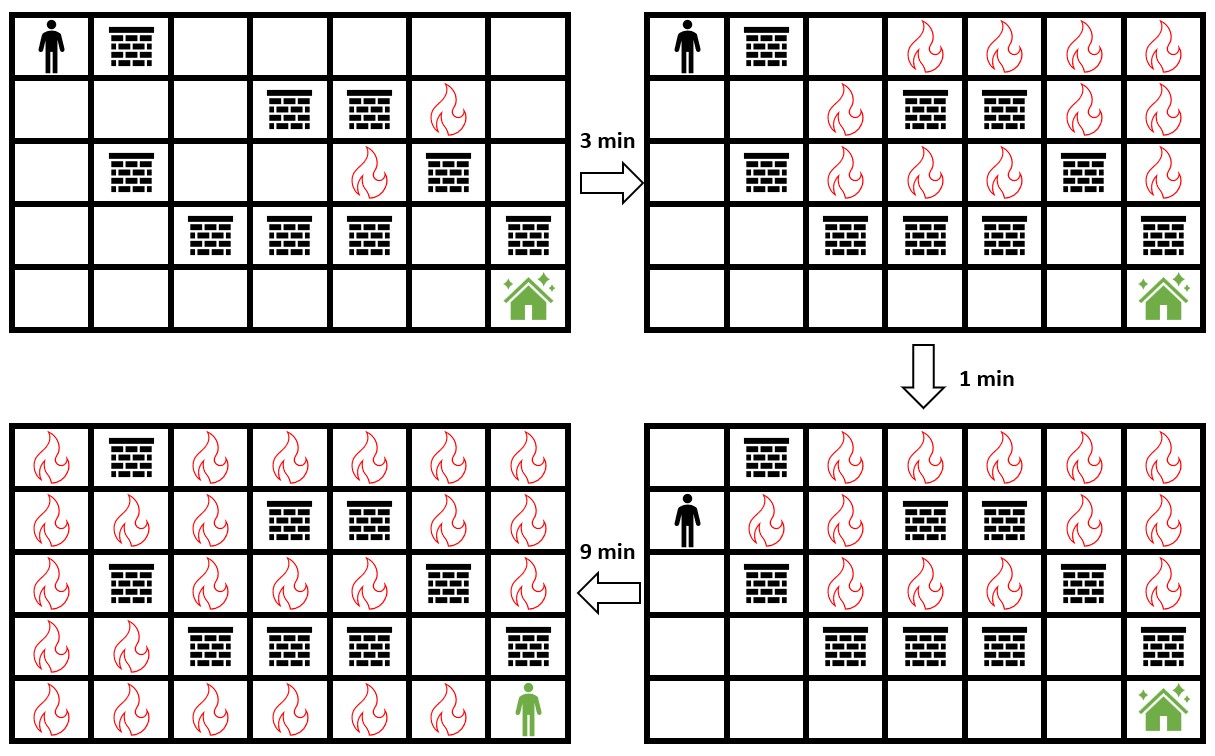
输入:grid = [[0,2,0,0,0,0,0],[0,0,0,2,2,1,0],[0,2,0,0,1,2,0],[0,0,2,2,2,0,2],[0,0,0,0,0,0,0]]
输出:3
解释:上图展示了你在初始位置停留 3 分钟后的情形。
你仍然可以安全到达安全屋。
停留超过 3 分钟会让你无法安全到达安全屋。
示例 2:
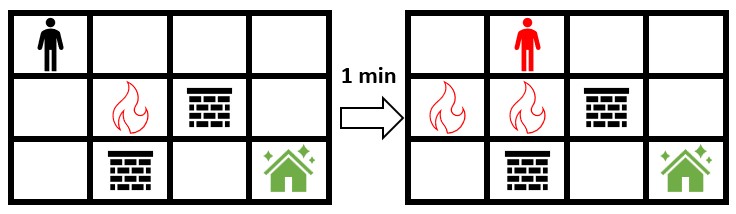
输入:grid = [[0,0,0,0],[0,1,2,0],[0,2,0,0]]
输出:-1
解释:上图展示了你马上开始朝安全屋移动的情形。
火会蔓延到你可以移动的所有格子,所以无法安全到达安全屋。
所以返回 -1 。
示例 3:
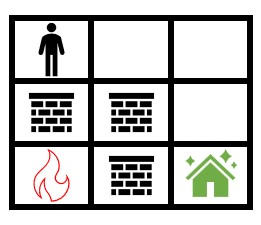
输入:grid = [[0,0,0],[2,2,0],[1,2,0]]
输出:1000000000
解释:上图展示了初始网格图。
注意,由于火被墙围了起来,所以无论如何你都能安全到达安全屋。
所以返回 109 。
提示:
m == grid.lengthn == grid[i].length2 <= m, n <= 3004 <= m * n <= 2 * 104grid[i][j] 是 0 ,1 或者 2 。grid[0][0] == grid[m - 1][n - 1] == 0
思路
题目为找人可以延迟多少分钟后再逃,即找最大延迟时间,设最大延迟时间为 t,只要在不超过 t 时间内这个人都是可以逃得掉的,那么这道题可以转化为找 t 时间,可以用二分查找。
解题方法
t 时间的范围为 0 到 m * n - 1,先求火在 t 时间蔓延有没有遇到人,如果没有遇到再让人和火一起赛跑,如果蔓延到人了就 GG 然后继续循环,直到找到最大的 t 时间。
复杂度
时间复杂度:
添加时间复杂度: check 时间复杂度 $O(mn)$,二分时间复杂度 $O(logmn)$
空间复杂度:
添加空间复杂度: $O(m * n)$
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
| class Solution {
int[][] dirs = new int[][]{{0, 1}, {0, -1}, {-1, 0}, {1, 0}};
int m, n;
boolean ok;
int[][] g, fg, pg;
public int maximumMinutes(int[][] grid) {
m = grid.length;
n = grid[0].length;
g = grid;
fg = new int[m][n];
pg = new int[m][n];
if (!check(0)) return -1;
int l = 0, r = m * n - 1;
while (l <= r) {
int mid = l + (r - l) / 2;
if (check(mid)) {
l = mid + 1;
} else {
r = mid - 1;
}
}
return r == m * n -1 ? (int)1e9 : r;
}
boolean check(int t) {
ok = false;
Queue<int[]> fire = new LinkedList<>();
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j ++) {
fg[i][j] = pg[i][j] = 0;
if (g[i][j] == 1) {
fg[i][j] = 1;
fire.offer(new int[]{i, j});
}
}
}
while(t-- > 0) update(fire, true, 0);
if (fg[0][0] != 0) return false;
Queue<int[]> people = new LinkedList<>();
pg[0][0] = 1;
people.offer(new int[]{0, 0});
while(!people.isEmpty()) {
update(fire, true, 1);
update(people, false, 1);
if (ok) return true;
}
return false;
}
void update(Queue<int[]> q, boolean isFire, int offset) {
int sz = q.size();
while (sz-- > 0) {
int[] info = q.poll();
int x = info[0], y = info[1];
for (int[] dir: dirs) {
int nx = x + dir[0], ny = y + dir[1];
if (nx < 0 || nx >= m || ny < 0 || ny >= n) continue;
if (g[nx][ny] == 2) continue;
if (isFire) {
if (fg[nx][ny] != 0) continue;
fg[nx][ny] = fg[x][y] + offset;
} else {
if (nx == m - 1 && ny == n - 1 && (fg[nx][ny] == 0 || fg[nx][ny] == pg[x][y] + offset)) ok = true;
if (fg[nx][ny] != 0 || pg[nx][ny] != 0) continue;
pg[nx][ny] = pg[x][y] + offset;
}
q.offer(new int[]{nx, ny});
}
}
}
}
|






