题目给出的条件为:图、路径有权值、权重无负数、求路径长度最值,可以使用 dijkstra 求 出发点 到其他点的 最短路径,记住dijkstra算法模板,直接套上用,构建一个 State类记录点的id和记录的最短路径长度,然后核心是最小堆,结合BFS遍历。
1334.阈值距离内邻居最少的城市
Problem: 1334. 阈值距离内邻居最少的城市
题目(点击展开)
有 n 个城市,按从 0 到 n-1 编号。给你一个边数组 edges,其中 edges[i] = [fromi, toi, weighti] 代表 fromi 和 toi 两个城市之间的双向加权边,距离阈值是一个整数 distanceThreshold。
返回能通过某些路径到达其他城市数目最少、且路径距离 最大 为 distanceThreshold 的城市。如果有多个这样的城市,则返回编号最大的城市。
注意,连接城市 i 和 j 的路径的距离等于沿该路径的所有边的权重之和。
示例 1:
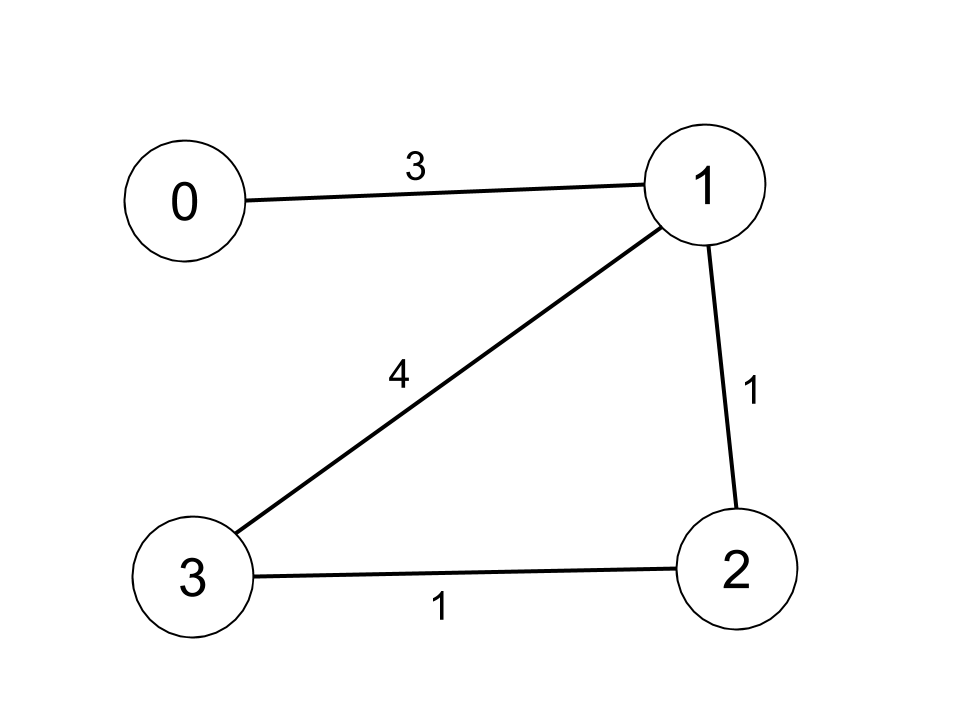
输入:n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
输出:3
解释:城市分布图如上。
每个城市阈值距离 distanceThreshold = 4 内的邻居城市分别是:
城市 0 -> [城市 1, 城市 2]
城市 1 -> [城市 0, 城市 2, 城市 3]
城市 2 -> [城市 0, 城市 1, 城市 3]
城市 3 -> [城市 1, 城市 2]
城市 0 和 3 在阈值距离 4 以内都有 2 个邻居城市,但是我们必须返回城市 3,因为它的编号最大。
示例 2:
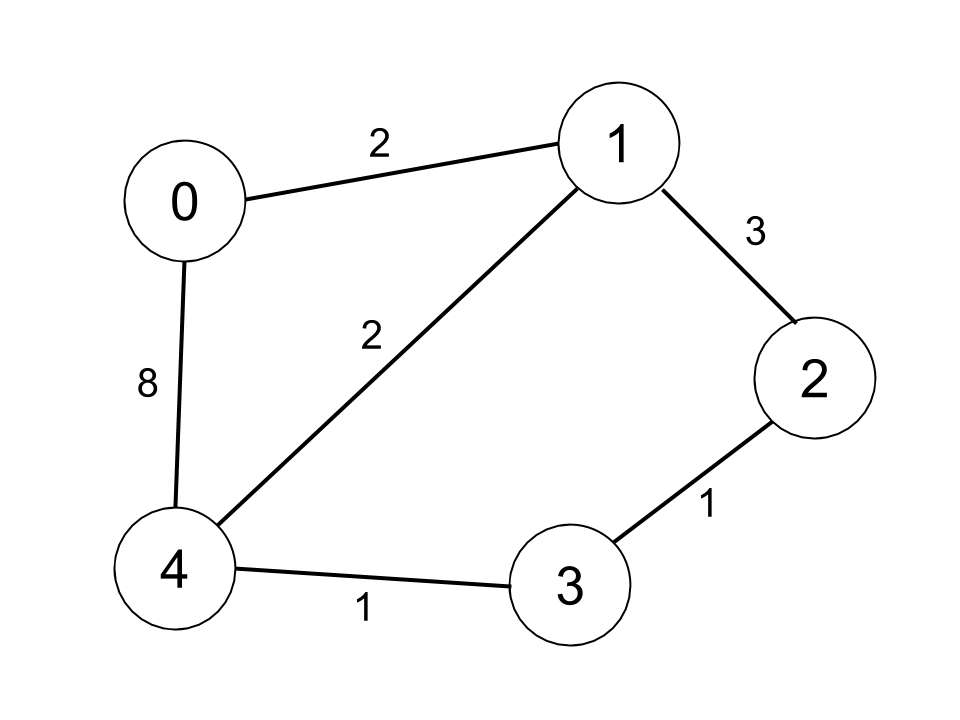
输入:n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2
输出:0
解释:城市分布图如上。
每个城市阈值距离 distanceThreshold = 2 内的邻居城市分别是:
城市 0 -> [城市 1]
城市 1 -> [城市 0, 城市 4]
城市 2 -> [城市 3, 城市 4]
城市 3 -> [城市 2, 城市 4]
城市 4 -> [城市 1, 城市 2, 城市 3]
城市 0 在阈值距离 2 以内只有 1 个邻居城市。
提示:
2 <= n <= 1001 <= edges.length <= n * (n - 1) / 2edges[i].length == 30 <= fromi < toi < n1 <= weighti, distanceThreshold <= 10^4- 所有
(fromi, toi) 都是不同的。
思路
图,有权值,权重无负数,求路径长度,可以使用dijkstra求出发点到其他点的最短路径。
解题方法
核心数据结构为求起点到不超过阈值的最短路径,然后遍历所有的点,求最短路径的长度,题目为求最后一个路径长度最短的点,遍历找到即可。
复杂度
添加空间复杂度, 示例: $O(n+m)$
- Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
| class Solution {
int max;
boolean[] visited;
public int findTheCity(int n, int[][] edges, int distanceThreshold) {
max = distanceThreshold;
visited = new boolean[n];
List<int[]>[] graph = new LinkedList[n];
for(int i = 0; i < n; i++) {
graph[i] = new LinkedList<>();
}
for(int[] edge: edges) {
int from = edge[0];
int to = edge[1];
int w = edge[2];
graph[from].add(new int[]{to, w});
graph[to].add(new int[]{from, w});
}
int ans = -1, cnt = n + 1;
for(int i = 0; i < n; i++) {
int[] dist = dijkstra(i, graph);
int cur = 0;
for (int j = 0; j < n; j++) {
if(i != j && dist[j] <= max) cur++;
}
if (cur <= cnt) {
cnt = cur;
ans = i;
}
}
return ans;
}
public int[] dijkstra(int start, List<int[]>[] graph) {
int[] dist = new int[graph.length];
Arrays.fill(dist, Integer.MAX_VALUE);
dist[start] = 0;
visited[start] = true;
Queue<State> pq = new PriorityQueue<>((a, b) -> {
return a.distance - b.distance;
});
pq.offer(new State(start, 0));
while(!pq.isEmpty()) {
State cur = pq.poll();
int curId = cur.id;
int curDistance = cur.distance;
if (curDistance > dist[curId] || curDistance > max) continue;
for(int[] neighbor: graph[curId]) {
int nextId = neighbor[0];
int nextW = dist[curId] + neighbor[1];
if (dist[nextId] > nextW) {
dist[nextId] = nextW;
pq.offer(new State(nextId, nextW));
}
}
}
return dist;
}
}
class State {
int id;
int distance;
public State(int _id, int _distance) {
this.id = _id;
this.distance = _distance;
}
}
|
787.K 站中转内最便宜的航班
Problem: 787. K 站中转内最便宜的航班
有 n 个城市通过一些航班连接。给你一个数组 flights ,其中 flights[i] = [fromi, toi, pricei] ,表示该航班都从城市 fromi 开始,以价格 pricei 抵达 toi。
现在给定所有的城市和航班,以及出发城市 src 和目的地 dst,你的任务是找到出一条最多经过 k 站中转的路线,使得从 src 到 dst 的 价格最便宜 ,并返回该价格。 如果不存在这样的路线,则输出 -1。
示例 1:
输入:
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 1
输出: 200
解释:
城市航班图如下
 从城市 0 到城市 2 在 1 站中转以内的最便宜价格是 200,如图中红色所示。
从城市 0 到城市 2 在 1 站中转以内的最便宜价格是 200,如图中红色所示。
示例 2:
输入:
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 0
输出: 500
解释:
城市航班图如下
 从城市 0 到城市 2 在 0 站中转以内的最便宜价格是 500,如图中蓝色所示。
从城市 0 到城市 2 在 0 站中转以内的最便宜价格是 500,如图中蓝色所示。
提示:
1 <= n <= 1000 <= flights.length <= (n * (n - 1) / 2)flights[i].length == 30 <= fromi, toi < nfromi != toi1 <= pricei <= 104- 航班没有重复,且不存在自环
0 <= src, dst, k < nsrc != dst
思路
图,带权值,没有负值,求起点和终点的最短路径,可以使用dijkstra。
解题方法
本题的难点在:求中转航班时,可能会出现死胡同而排除掉正确的答案,比如用例
n=5,flights=[[0,1,5],[1,2,5],[0,3,2],[3,1,2],[1,4,1],[4,2,1]],src =0,dst=2,如果用默认的dijkstra框架,遇到 curW > dist[curId]就剪枝,会把正确答案给排除掉,比如到终点的路径应该是0-1-4-2得7,而返回的却是0-3-1-2得9,在dist[1]=4已经把[0,1,5]这个航班剪掉了,所以我们要用可以中转航班次数来作为剪枝条件,把 curW > dist[curId] 改为 curK < 0,然后如果遇到还有中转次数时,也要把该点入堆。
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
| class Solution {
public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
List<int[]>[] graph = new LinkedList[n];
for(int i = 0; i < n; i++) {
graph[i] = new LinkedList<>();
}
for(int[] flight: flights) {
int from = flight[0];
int to = flight[1];
int w = flight[2];
graph[from].add(new int[]{to, w});
}
int[] dist = dijkstra(graph, src, dst, k);
return dist[dst] != Integer.MAX_VALUE ? dist[dst] : -1;
}
public int[] dijkstra(List<int[]>[] graph, int src, int dst, int k) {
Queue<State> pq = new PriorityQueue<>((a, b) -> {
return a.distance - b.distance;
});
pq.offer(new State(src, 0, k));
int[] dist = new int[graph.length];
int[] stop = new int[graph.length];
Arrays.fill(dist, Integer.MAX_VALUE);
while(!pq.isEmpty()) {
State cur = pq.poll();
int curId = cur.id;
int curW = cur.distance;
int curK = cur.k;
if (curId == dst) {
return dist;
}
if (curK < 0) {
continue;
}
for(int[] neighbor: graph[curId]) {
int nextId = neighbor[0];
int nextW = curW + neighbor[1];
int nextK = curK - 1;
if (dist[nextId] > nextW) {
dist[nextId] = nextW;
pq.offer(new State(nextId, nextW, nextK));
stop[nextId] = nextK;
} else if (stop[nextId] < nextK) {
pq.offer(new State(nextId, nextW, nextK));
}
}
}
return dist;
}
}
class State {
int id;
int distance;
int k;
public State(int _id, int _distance, int _k) {
this.id = _id;
this.distance = _distance;
this.k = _k;
}
}
|
882. 细分图中的可到达节点
Problem: 882. 细分图中的可到达节点
给你一个无向图(原始图),图中有 n 个节点,编号从 0 到 n - 1 。你决定将图中的每条边 细分 为一条节点链,每条边之间的新节点数各不相同。
图用由边组成的二维数组 edges 表示,其中 edges[i] = [ui, vi, cnti] 表示原始图中节点 ui 和 vi 之间存在一条边,cnti 是将边 细分 后的新节点总数。注意,cnti == 0 表示边不可细分。
要 细分 边 [ui, vi] ,需要将其替换为 (cnti + 1) 条新边,和 cnti 个新节点。新节点为 x1, x2, ..., xcnti ,新边为 [ui, x1], [x1, x2], [x2, x3], ..., [xcnti-1, xcnti], [xcnti, vi] 。
现在得到一个 新的细分图 ,请你计算从节点 0 出发,可以到达多少个节点?如果节点间距离是 maxMoves 或更少,则视为 可以到达 。
给你原始图和 maxMoves ,返回 新的细分图中从节点 0 出发 可到达的节点数 。
示例 1:

输入:edges = [[0,1,10],[0,2,1],[1,2,2]], maxMoves = 6, n = 3
输出:13
解释:边的细分情况如上图所示。
可以到达的节点已经用黄色标注出来。
示例 2:
输入:edges = [[0,1,4],[1,2,6],[0,2,8],[1,3,1]], maxMoves = 10, n = 4
输出:23
示例 3:
输入:edges = [[1,2,4],[1,4,5],[1,3,1],[2,3,4],[3,4,5]], maxMoves = 17, n = 5
输出:1
解释:节点 0 与图的其余部分没有连通,所以只有节点 0 可以到达。
提示:
0 <= edges.length <= min(n * (n - 1) / 2, 104)edges[i].length == 30 <= ui < vi < n- 图中 不存在平行边
0 <= cnti <= 1040 <= maxMoves <= 1091 <= n <= 3000
思路
这是最短路径的变种题,在求不超过阈值的范围内的最短路径,还要新加一层判断不能到的地方还能多走几步
解题方法
核心算法dijkstra不需要变,但是需要改变一下题目所给的权重,因为权重仅包含中间出现的节点,未包含上一个图的节点,所以初始化图的时候 w 需要 +1。
然后核心的关键在于求所有的节点:所有的总数 = maxMoves步数内能到达的点的个数 + 中间的还有几个节点可以走
- Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
| class Solution {
public int reachableNodes(int[][] edges, int maxMoves, int n) {
List<int[]>[] graph = new LinkedList[n];
for(int i = 0; i < n; i++) {
graph[i] = new LinkedList<>();
}
for(int[] edge: edges) {
int from = edge[0];
int to = edge[1];
int w = edge[2] + 1;
graph[from].add(new int[]{to, w});
graph[to].add(new int[]{from, w});
}
int[] dist = dijkstra(graph, 0);
int ans = 0;
for(int i = 0; i < n; i++) {
if (dist[i] <= maxMoves) {
ans ++;
}
}
for(int[] edge: edges) {
int from = edge[0];
int to = edge[1];
int w = edge[2];
int a = Math.max(maxMoves - dist[from], 0);
int b = Math.max(maxMoves - dist[to], 0);
ans += Math.min(a + b, w);
}
return ans;
}
public int[] dijkstra(List<int[]>[] graph, int start) {
int[] dist = new int[graph.length];
Arrays.fill(dist, Integer.MAX_VALUE);
Queue<State> pq = new PriorityQueue<>((a, b) -> {
return a.dis - b.dis;
});
dist[start] = 0;
pq.offer(new State(start, 0));
while(!pq.isEmpty()) {
State cur = pq.poll();
int curId = cur.id;
int curW = cur.dis;
if (curW > dist[curId]) continue;
for(int[] neighbor: graph[curId]) {
int nextId = neighbor[0];
int nextW = neighbor[1] + curW;
if (dist[nextId] > nextW) {
dist[nextId] = nextW;
pq.offer(new State(nextId, nextW));
}
}
}
return dist;
}
}
class State {
int id;
int dis;
public State(int _id, int _dis) {
this.id = _id;
this.dis = _dis;
}
}
|


从城市 0 到城市 2 在 1 站中转以内的最便宜价格是 200,如图中红色所示。
从城市 0 到城市 2 在 0 站中转以内的最便宜价格是 500,如图中蓝色所示。




