并查集，求连通分量和拓扑排序等问题

图，求连通分量，判断点与点是否连通，求拓扑排序等问题，可以使用并查集去解决问题。

并查集模板

class UF {
    private int[] parent;
    private int count;

    public UF(int n) {
        count = n;
        parent = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
    }
    public int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }

    public void union(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);
        if (rootP == rootQ) {
            return;
        }
        parent[rootQ] = rootP;
        count --;
    }
    public boolean connect(int p, int q) {
        return find(p) == find(q);
    }
}

684.冗余连接

Problem: 684. 冗余连接

树可以看成是一个连通且无环的无向图。

给定往一棵 n 个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [a_i, b_i] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的那个。

示例 1：

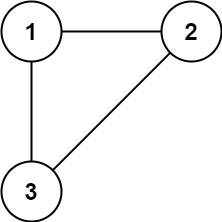
输入: edges = [[1,2], [1,3], [2,3]]
输出: [2,3]

示例 2：

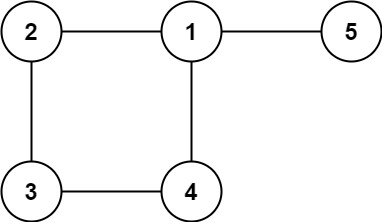
输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]]
输出: [1,4]

提示:

n == edges.length
3 <= n <= 1000
edges[i].length == 2
1 <= ai < bi <= edges.length
ai != bi
edges 中无重复元素
给定的图是连通的

思路

题目的题意一开始的图就是一个连通图，那么求可以删除的最后一条边，即所有给出的边连接成一个连通图有哪条边是多余的可以不拿来连接。
解题方法

把给出的边拿来做并查集构建连通图，如果哪条边是多余的（即connect为true），并且求是最后一个connect 为true，即为答案。
复杂度

时间复杂度:

循环n个点$O(n)$，并查集$O(logn)$，时间复杂度共$O(nlogn)$
空间复杂度:

$O(n)$

Code

class Solution {
    public int[] findRedundantConnection(int[][] edges) {
        int n = edges.length;
        UF graph = new UF(n);
        int[] ans = new int[2];
        for (int[] edge: edges) {
            int a = edge[0] - 1;
            int b = edge[1] - 1;
            // System.out.println(graph.connect(a, b));
            if (graph.connect(a, b)) {
                ans = new int[]{a + 1, b + 1};
            } else {
                graph.union(a, b);
            }
        }
        return ans;
    }
}

class UF {
    private int[] parent;
    private int count;

    public UF(int n) {
        count = n;
        parent = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
    }
    public int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }

    public void union(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);
        if (rootP == rootQ) {
            return;
        }
        parent[rootQ] = rootP;
        count --;
    }
    public boolean connect(int p, int q) {
        return find(p) == find(q);
    }
}